內容目錄
1. 何謂散佈圖
散布圖(scatter plot / scatter graph)是用來研究兩變數間之相關聯性(正相關、負相關、或無相關)。它是在方格紙上以縱軸表示結果,以橫軸表示原因;然後用點表示出分佈形態根據分佈的形態來判斷對應數據之間的相互關係(圖1)。此外也可以顯示出相異資料之間之層別的情況。如:鋼的粹火溫度和硬度、鏍釘的轉距和抗張力、油的溫度與粘度等。

這裡講的數據是成對的,一般來說成對數據有三種不同的對應關係。
- (a) 原因與結果數據關係。
- (b) 結果與結果數據關係。
- (c) 原因與原因數據關係。
2. 散佈圖製作的五個步驟
- (a) 收集相對應數據,至少30組上,並且整理寫到數據表上。
- (b) 找出數據之中的最大值和最小值。
- (c) 書出縱軸與橫軸刻度,計算組距。
- (d) 將各組對應數據標示在座標上。
- (e) 記入必要事項。
3. 散佈圖的研判
散佈圖的研判一般來說有六種形態。
(3-1) 正相關
在圖中當X增加,Y也增加,也就是表示原因與結果有相對的正相關(圖2)。

(3-2) 弱正相關
散佈圖點的分佈較廣但是有向上的傾向,這個時候X增加,一般Y也會曾加,但非相對性,也就是說X除了受Y的因素影響外,可能還有其他因素影響著X,有必要進行其他要因再調查,這種形態叫做似有正相關稱為弱正相關 (圖3)。

(3-3) 負相關
當X增加,Y反而減少,而且形態呈現一直線發展的現象,這叫做負相關(圖4)。

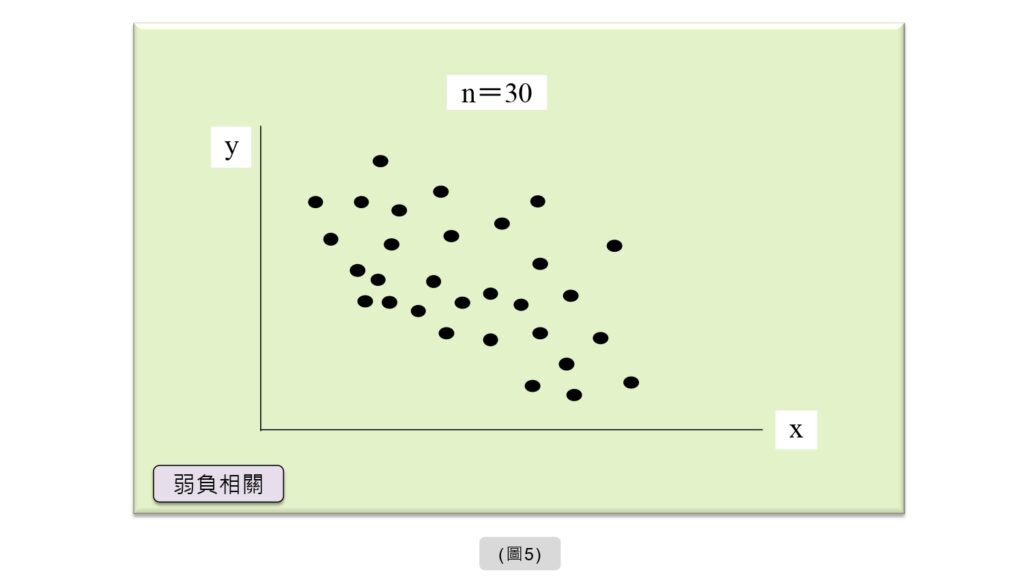
(3-4) 弱負相關
當X增加,Y減少的幅度不是很明顯,這時的X除了受Y的影響外,尚有其他因素影響X,這種形態叫做弱負相關(圖5)。
(3-5) 無相關
如果散佈點的分佈呈現雜亂,沒有任何傾向時,稱為無相關(圖6),也就是說X與Y之間沒有任何的關係,或X增大時,Y并不改變,這時應再一次先將數據層別化之後再分析。

(3-6) 曲線相關
假設X增大,Y也隨之增大,但是X增大到某一值之后,Y反而開始減少,因此產生散佈圖點的分佈有曲線傾向的形態,稱為曲線相關(圖7)。

4. 散佈圖判讀注意事項
- (a) 注意有無異常點;異常點應查明原因后再刪除,異常點多,可能為測定誤差或混入不良品等特別原因所引起。
- (b) 是否有層別必要;全體看不出有何相關,層別后可看出相關關係存在,反之亦然。
- (c) 是否為假相關;依據技術經驗認為沒有相關,但經散佈圖分析卻有相關趨勢,宜進一步檢討有否任何原因造成假相關?
- (d) 勿依據技術,經驗作直覺判斷。
- (e) 數據太少,容易發生誤判。
- (f) 調查有無異常原因。如X與Y可能有正相關關係,但中間之空隙部份必存在特殊原因,需加以調查,方能找出結論。
5. 散佈圖實例
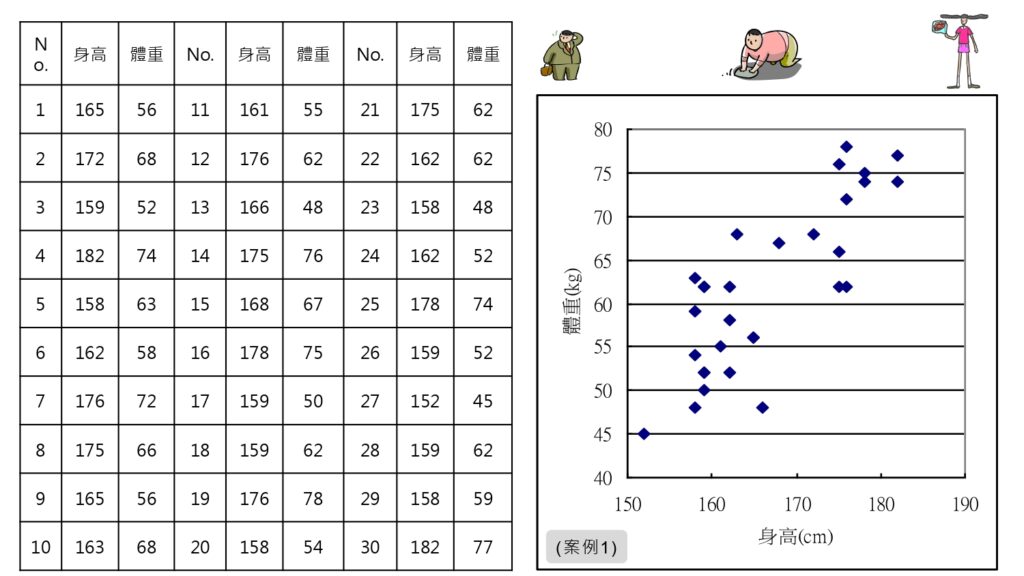
(5-1) 例1
☆ 其他參考資料及文章
★ 【QC七大手法及其應用】(按圖超連結)